Home

Works × Notes × LinkedIn × StackOverflow × Github

Algorithmes distribués

Caractéristiques typiques des systèmes distribués

  1. Ils sont composés de plusieurs processus
  2. Les processus communiquent par des messages
  3. Ils ont des espaces de mémoire disjoints
  4. Le système a une tache collective à réaliser

Problèmes algorithmiques typiques

Modèle de système distribué synchrone

Chaque processus i est composé de:

Notes:

1. Problème d’élection de leader

1.1. Sur un Token Ring

Hypothèses

  1. Anneau unidirectionnel SYNCHRONISÉ
  2. Chaque processus a un identificateur unique (de l’ensemble UID de tous les identificateurs possibles)
  3. L’anneau est orienté: Chaque processus connait le lien suivant dans le sens des aiguilles d’une montre, noté $lien_+$, et le lien inverse noté $lien_-$

Problème d’élection de leader

Supposons que chaque processus i a une variable nommée état tq, état $\in$ {leader, inconnu}.

A la terminaison de l’exécution d’un algorithme résolvant le problème, il faut qu’exactement 1 processus ait sa variable état à la valeur leader.

Variante (a) du problème: Tout les processus sauf 1 seul se rendent compte qu’ils ne sont pas leader

Variante (b) du problème: Pendant toute l’exécution il y a au plus un leader

1.1.1. Algorithme LCR (Lelann-Chang-Roberts)

Alphabet: M = UID = ensemble des id possibles

Pour tout processus i: States$_i$ et Start$_i$:

msgs$_i$:

trans$_i$:

msg := null
v := message reçu
Si u=/=null, on regarde v:
    cas v=u:
        état:=leader
        msg:=u
        u:=null
    cas v>umax:
        msg:=v
        umax:=v
    cas v=umax:
        état:=inconnu  !ou non_leader
        msg:=v
        !u:=null facultatif

Autre version (utilisée pour les calculs de complexité dans la partie suivante): on ne garde pas de umax mais le leader va envoyer un message spécifique pour signaler son élection, contenant son id ainsi qu’un tag leader.

Complexité du LCR

On ignore les n rounds/messages nécessaires pour que le processus élu leader l’annonce aux autres.

type pire cas meilleur cas
temps (rounds) ~$2n$ rounds, soit $O(n)$ rounds =
mémoire/processus $O(1)$ =
communication (messages) ~$n\dfrac{n+1}{2}$, soit $O(n²)$: cas où les ids sont ordonnés par ordre décroissants ~$2n$, soit $O(n)$: ids ordonnés par ordre croissant

Indication de preuve de correction:

Lèmme 1.1: Un processus imax (i est l’indice, pas l’id) avec id maximum, noté umax, passe son état:=leader à la fin du nème round

Lèmme 1.2: $\forall$r tq 0 $\leq$ r $\leq$ n-1, après r rounds, msg(imax + r) mod n = umax, par récurrence sur r

Lèmme 2.1: $\forall$ processus i tq i $\neq$ imax, l’action état:=leader n’est jamais effectuée

Lèmme 2.2: $\exists$ un processus j $\in$ [i+1, imax], tq au round (j - i) mod n, msgj $\neq$ ui

Théorème

Dans un anneau de taille n $>$ 1, si tous les processus sont identiques (même code, même nom) il n’existe pas un algorithme d’élection de leader même si n est connu et si l’anneau est bidirectionnel.

Preuve: Par l’absurde: Supposons qu’un tel algorithme existe. Considérons leur exécution: C0M1C1…

Tous les processus sont initialisés avec le même état s0.

Alors: à chaque round r: tous les processus prennent un nouvel état identique. Donc si au round n un leader a été élu, c’est que tous les processus sont leader, ce qui est interdit par l’énoncer du problème, donc l’algorithme résolvant le problème ne le résout pas: preuve par l’absurde qu’un tel algorithme n’existe pas !

1.1.2. Algorithme TS (Time Slice)

Hypothèse

Description du déroulement

Pour tout processus i: States$_i$ et Start$_i$:

msgs$_i$:

trans$_i$:

msg:=null
round:=round+1
Si round=n:
    round:=0
    étape:=étape+1
Si un message id_leader=/=u est reçu sur le lien_moins:
    leader:=id_leader 
    msg:=id_leader
Sinon:
    Si round=(v-1)n+1:
        leader:=u
        msg:=u

Variante: Élection du plus grand id

Attributs supplémentaires/modifiés dans Statesi:

trans$_i$:

msg:=null
Si leader=inconnu:
    round:=round+1
    Si round=n:
        round:=0
        étape:=étape+1
    Si un message ui est reçu sur le lien_moins:
        leader:=ui
        msg:=ui
    Sinon:
        Si un message ping est reçu sur le lien_moins:
            compteur_processus:=compteur_processus+1
            msg:=ping
        Si compteur_processus=n-1:
            leader:=u
            msg:=u
        Si round=(v-1)n+1:
            msg:=ping

Comparatif complexités

type id le plus petit Variante: id le plus grand
temps (rounds) $O(n.id_{min})$ $n.id_{max-1}+distance: entre:processus_{id_{max}} et: processus_{id_{max−1}} = O(n.id_{max−1}))$
mémoire/processus $O(1)$ $O(1)$
communication (messages) $O(n)$ $O(n^2)$

Note: $id_{max-1}$ est le 2ème plus grand id.

1.1.3. Algorithme HS (Hirschberg-Sinclair)

Nouvelle Hypothèse

Fonctionnement

L’ensemble des messages contient les triplets composés d’un id $\in$ UID, d’un flag $\in$ {out, in}, et d’un entier positif k $\in \mathbb{N}$+ qui est le compteur de sauts.

Un message $\in$ UID x {out, in} x $\mathbb{N}$+ $\forall$ processus i:

Statesi & Startsi :

msgsi: renvoie msg+ sur lien+ et msg- sur lien-. transi:

msg_plus:=null; msg_moins:=null
Si le message reçu est (v, out, h) sur lien_moins alors:
    cas v>u et h>1: msg_plus:=(v, out, h-1)
    cas v>u et h=1: msg_moins:=(v, in, 1)
    cas v=u: état:=leader
Si le message reçu est (v, out, h) sur lien_plus alors:
    cas v>u et h>1: msg_moins:=(v, out, h-1)
    cas v>u et h=1: msg_plus:=(v, in, 1)
    cas v=u: état:=leader
Si le message reçu est (v, in, 1) sur lien_moins et v>u alors:
    !Comment: ici v!=u suffit puisque v<u impossible avec tag in
    msg_plus:=(v, in, 1)
Si le message reçu est (v, in, 1) sur lien_plus et v>u alors:
    !Comment: ici v!=u suffit puisque v<u impossible avec tag in
    msg_moins:=(v, in, 1)
Si le message reçu est (u, in, 1) sur les deux liens alors:
    phase:=phase + 1
    msg_plus:=(u, out, 2**phase)
    msg_moins:=(u, out, 2**phase)

Complexité de l’algorithme HS

En communication

Le processus i passe à la phase l ssi dans la phase précédente l-1 il n’y a pas de processus avec un id plus grand que idi parmis les processus à une distance $d = 2^{l-1}$ de i.

Au plus $\lfloor\dfrac{n}{2^{l-1}+1}\rfloor$ processus passent à la phase l.

Ils envoient au plus $2.2.2^{l}\lfloor\dfrac{n}{2^{l-1}+1}\rfloor = O(n)$ messages durant cette étape Le nombre de phases est $O(log(n))$ $\Rightarrow$ complexité en messages = $O(n.log(n))$

En temps

$O(n.log(n))$ très grossièrement. Analyse plus poussée: Dans chaque phase l, chaque processus qui envoie les messages les envoie à la distance $2.2^{l}$ au plus: \(2.(1+2+4+8+...+2^{O(log(n))}) \\ = 2.(2.\dfrac{1 - 2^{O(log(n))}}{-1} + 2^{O(log(n))}) \\ = O(2^{O(log(n))}) = O(n)\)

1.2. Sur un graphe connexe

Les Hypothèses

  1. Graphe de communication connexe quelconque
  2. Chaque processus a un identificateur unique (de l’ensemble UID de tous les identificateurs possibles)
  3. Communication synchronisée
  4. le diamètre du graphe est connu par les processus

Définitions

Distance entre deux nœuds: Longueur du plus court chemin entre deux nœuds. Diamètre d’un graphe: Plus grande distance entre deux nœuds du graphe.

Pour chaque processus i (un processus par nœud) States$_i$ & Starts$_i$:

msgs$_i$: Si $round < diamètre$, envoyer $u_{max_i}$ à tous les processus j voisins trans$_i$:

round:=round+1
Soit W l ensemble des id reçus dans ce round
max_id:=MAX({max_id} + W)
Si round:=diametre alors:
    Si max_id=u alors état:=leader
Sinon état:=non_leader

Complexités

Communication

$Comp_{messages} = diametre.2.|E|$

avec $E$ = nombre d’arêtes

Temps

$Comp_{round} = diametre$

2. Problème de consensus sur un graphe complet

Hypothèses

Problème d’accord/de consensus

  1. Agrément: Deux processus ne se décident pas pour deux valeurs différentes.
  2. Validité: Si tous les processus ont la même valeur initiale v, alors v est la seule décision possible
  3. Terminaison: Tout processus non-défaillant finit par décider une valeur

/!\ La décision ne se fait qu’une seule fois !

Notes: Problème simple à résoudre si tout va bien, i.e. sans défaillance: On partage les valeur et on décide pour la valeur maximum ou la valeur la plus présente (avec max choisi si égalité) par exemple.

2.1. Consensus avec des défaillances d’arrêt (crash)

Notes:

Exemple de crash problématique:

fig1

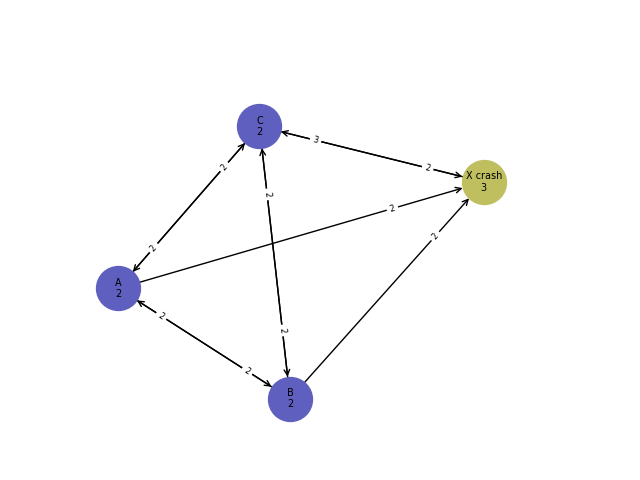
Le processus X va par exemple crasher (hypothèse: les crash sont définitifs) après n’avoir eu le temps d’envoyer sa valeur $v_0$ qu’au processus C.

Théorème

Il est impossible de résoudre le problème de consensus dans un réseau asynchrone pouvant subir des défaillances d’arrêt.

Asynchrone = Il est impossible de borner le temps de parcours des messages

Intuition du problème : Les arrêtes sortantes du processus x sont très lentes et les autres processus vont décider avant de recevoir les messages de x.

Le problème se résout grâce à l’hypothèse f $<$ n (cf suite)

2.1.1. Algorithme de FloodSet

Pour chaque processus i:

Les éléments de M (ensemble de messages possibles) sont des ensembles de valeur dans U (ensemble des valeurs initiales)

$M = \mathbb{P}(U)$

States$_i$ & Starts$_i$:

msgs$_i$: Si rounds $\leq$ f alors envoie W à tout les autres processus, sinon leur envoie null trans$_i$:

rounds:=round+1
Soit Wj le message qui arrive du voisin j
Pour tout voisin j:
    W = Wj U W
Si (rounds = f+1) alors:
    Si |W|=1 alors:
        décision:=v tq W={v}
    Sinon:
        décision:=v0 
        !aurait pu être aussi le Max(W) 
        !par exemple si une valeur v0 commune n'était 
        !pas disponible

La correction de l’algorithme FloodSet repose sur 2 points principaux:

  1. Parmi les f+1 premiers rounds, au moins un est sans défaillances (hypothèse $f<n$)
  2. À la fin d’un round sans défaillances, chaque processus correct obtient le même ensemble $W_2$ et à partir de ce round $\forall$ processus $i, W_i$ ne change plus.
Complexité

$Comp_{rounds}\leq f+1 = O(f)$ messages

$Comp_{messages}\leq n.(n-1).(f+1) = O(fn²)$ messages

Chaque message inclus au maximum n valeurs ($|W|\leq n$) et chaque valeur de b bits $Comp_{bits:transmis} \leq n^3bf = O(fn^3)$

2.1.3. Algorithme de FloodSet optimisé

Pour chaque processus i:

Les éléments de M (ensemble de messages possibles) sont des ensembles de valeur dans U (ensemble des valeurs initiales)

$M = \mathbb{P}(U)$

States$_i$ & Starts$_i$:

msgs$_i$: Envoyer msg à tous les voisins trans$_i$:

msg:=null
rounds:=round+1
Soit wj le message qui arrive du voisin j
Pour tout voisin j: 
    Ajoute w à W
Si (rounds = f+1) alors:
    Si |W|=1 alors:
        décision:=v tq W={v}
    Sinon:
        décision:=v0 
        !Contrairement au cas du floodset simple,
        !on ne peux pas remplacer cette ligne par décision:=Max(W) 
        !puisque les Wi peuvent être différents !
Sinon si |W|>1 et done=false:
    done:=true
    msg:=v, tq v appartient à W et v=/=w

L’idée est que la première fois où un processus reçoit une valeur différente de la sienne, il avertisse les n autres processus de cette valeur. Il n’envoie qu’une seule valeur (et pas un set) et cela, une unique fois (et pas à chaque round).

Comparatif de complexités
Complexité FloodSet simple FloodSet optimisé
$Comp_{rounds}$ $O(f)$ $O(f)$
$Comp_{messages}$ $O(fn^2)$ $n.n$ messages sont envoyés au premier round, puis dans le pire cas (tous les processus n’ont pas le même u) tout les processus vont envoyer une fois de plus un message à chaque autre processus, d’où une complexité de: $2n^2 = O(n^2)$
$Comp_{bits:transmis}$ $O(fn^3)$ $2bn^2 = O(n^2)$

2.2. Consensus avec des défaillances Byzantines

Définition

Un processus présentant une défaillance byzantin est un processus que l’on considère libre d’adopter un comportement non conforme.

Les défaillances Byzantines sont plus générales que les défaillances d’arrêt.

Une résolution avec défaillances Byzantines résout n’importe quel problème de défaillances d’arrêt dans les mêmes conditions.

Problème

  1. Agrément: Deux processus non-défaillants ne se décident pas pour deux valeurs différentes.
  2. Validité: Si tous les processus non-défaillants ont la même valeur initiale v, alors v est la seule décision possible
  3. Terminaison: Tout processus non-défaillants finit par décider une valeur

Théorème

Le problème du consensus Byzantin ne peut pas être résolu avec $f>\dfrac{n}{3}$ processus Byzantins

Exemple

$n=4, f=1$ $::::::$ ($1<\dfrac{4}{3}$) fig2

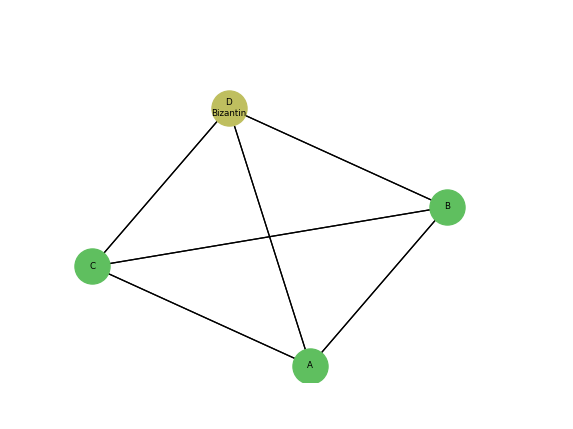
Considérons l’algorithme de consentement suivant: States & Starts:

msgs$_i$: envoyer $v_i$ à tous les processus, y compris i trans$_i$:

Si n messages reçus alors:  !y compris le message de i vers i
    Calculer la valeur majoritaire mi (la plus petite en cas d'=)
    vi:=mi

Voici un exemple de comportement du processus Bizantin qui casse cet algorithme: 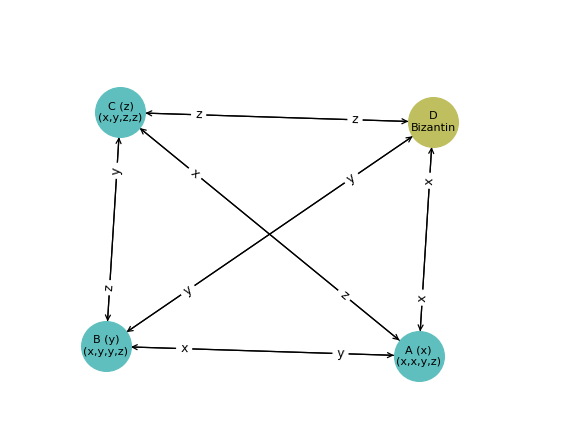fig3 $\rightarrow$ Le Bizantin envoie des valeurs différentes aux trois autres processus. $\rightarrow$ Ce comportement fait décider des valeurs différentes à A, B et C : $x \neq y \neq z$

2.2.1. Diffusion Fiable avec maréchal

Hypothèse
Déroulement

Note: On considère que le processus Bizantin est obligé d’envoyer un et un seul message aux moments où il est sensé le faire pour ne pas révéler son dysfonctionnement aux autres.

On distingue deux cas pour intuiter de la solidité de ce scénario: Cas 1: Le maréchal n’est pas Bizantin fig4

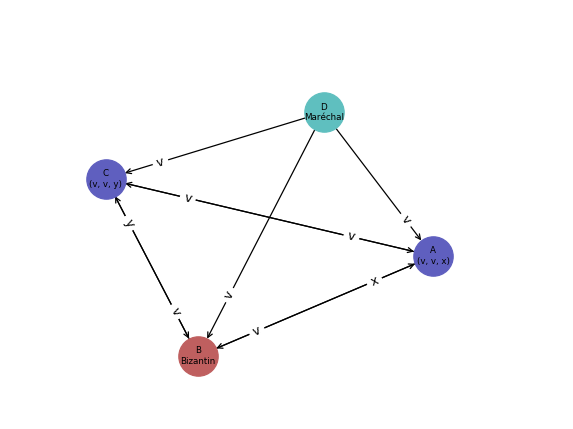
  1. Le Bizantin est un processus lambda.
  2. Le maréchal va envoyer le message v à A, B et C.
  3. Le maréchal va tenter de casser le déroulement du consensus en envoyant des valeurs différentes x et y à A et C.
  4. Au final D qui est maréchal décide de la valeur v dont il a réalisé la diffusion initialement. Les deux autres processus non défectueux décident également la valeur v qui est la valeur médiane dans le set de valeurs obtenu par chacun.

Cas 2: Le maréchal est Bizantin fig5

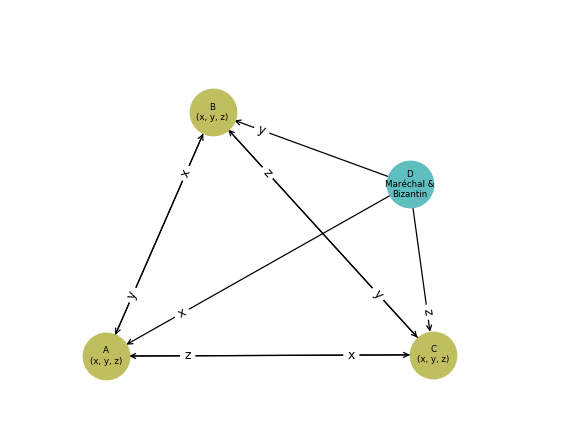
  1. Le Bizantin est le processus maréchal.
  2. Le maréchal va tenter de casser le déroulement du consensus en envoyant des valeurs différentes x, y et z à A, B et C.
  3. Les processus A, B et C s’échangent ensuite leurs valeurs.
  4. Les trois processus non défectueux A, B et C ont au final des set de valeurs identiques et décident tous la même valeur médiane y.

2.2.2. Diffusion Fiable sans maréchal

Hypothèse
Complexités

$comp_{temps} = O(1)$ $comp_{messages} = O(n^2)$ $comp_{bits:transmis} = O(n^3)$ $comp_{memoire/processus} = O(n)$

3. Diffusion d’information/Construction d’arbre BFS sur un graphe connexe

Définition

Arbre BFS (Breadth-First Search): C’est un arbre couvrant possédant un nœud spécial nommé racine $r_0$ et tel que la distance de tout les nœuds avec $r_0$ est la même que dans le graphe sous-jacent

Pour chaque processus i (un processus par nœud) States$_i$ & Starts$_i$:

msgs$_i$: envoyer $msg_i$ à tous les processus j voisins trans$_i$:

msg:=null
Si deja_vu=false et message m reçu sur le canal p:
    msg:=m
    deja_vu:=true
    pere:=p

Complexités

Communication:

$Comp_{messages} = n.E(nombreDeVoisins)=2.\vert E\vert$ avec $n=nombreDeNœuds$

Dans le cas de l’optimisation “On ne réponds pas à son père”, $Comp_{messages} = 2.\vert E\vert - (n-1)$

Dans le cas de l’optimisation “On connait ses fils”, $Comp_{messages} = n- 1$

Temps:

$Comp_{round} = profondeur$

5. Références

Cours écrit par Enzo Bonnal et basé sur: